Dopasowanie krzywej w Pythonie

Czym jest dopasowanie krzywej?

Dopasowanie krzywej to metoda polegająca na znalezieniu funkcji matematycznej, która pasuje do danej serii punktów najlepiej według przyjętego kryterium. Metoda ta jest często stosowana w wielu dziedzinach inżynierii, nauki czy ekonomii w sytuacjach, w których chcemy znaleźć związek między dwiema zmiennymi, najlepiej w postaci y = f(x). Zazwyczaj dane, z którymi mamy do czynienia obarczone są pewnym błędem, dlatego funkcja nie musi przechodzić dokładnie przez wszystkie punkty. Zamiast tego, szukamy przybliżonej funkcji, która opisuje serię danych jako całość z najmniejszym błędem. Jednym ze sposobów minimalizacji całkowitego błędu jest metoda najmniejszych kwadratów, którą krótko omówię w dalszej części tego artykułu. Poniżej przedstawię najpopularniejsze funkcje stosowane w dopasowaniu krzywej, a następnie jak zaimplementować dopasowanie poszczególnych funkcji w języku Python.

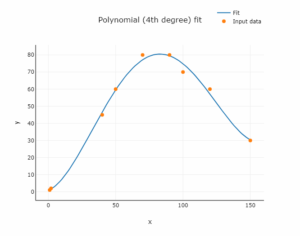
Wielomian

Zależność między zmienną niezależną x i zmienną zależną y ma postać wielomianu x n-tego stopnia. Regresję wielomianową można sklasyfikować w następujący sposób:

Funkcja liniowa – jeśli stopień wielomianu wynosi 1. Równanie funkcji dopasowania wygląda następująco:

$y = a + b \cdot x$

2. Funkcja kwadratowa – jeśli stopień wielomianu wynosi 2. Równanie wielomianu wygląda następująco:

$y = a_2 \cdot x^2 + a_1 \cdot x + a_0$

3. Funkcja sześcienna — jeśli stopień wynosi 3:

$y = a_3 \cdot x^3 + a_2 \cdot x^2 + a_1 \cdot x + a_0$

i tak dalej. Rząd wielomianu może być ogólnie n.

Regresja wielomianowa (wielomian czwartego stopnia)

Funkcja wykładnicza

W regresji wykładniczej wykorzystujemy następującą funkcję:

$y = a \cdot exp(b \cdot x)$

Funkcja potęgowa

Funkcja potęgowa ma następującą postać:

$y = a \cdot x^b$

Regresja logistyczna z czterema parametrami

W modelowaniu wielu układów biologicznych często stosuje się czteroparametrową regresję logistyczną (4PL). W wyniku dopasowania uzyskuje się krzywą w kształcie litery S. Wzór używany do dopasowania jest następujący:

$y = d+\frac{a-d}{1+(\frac{x}{c})^{b}}$

Gdzie:
a – minimalna wartość, jaką można uzyskać (y przy x = 0)
b – współczynnika Hilla
c – punkt przegięcia (tj. punkt na krzywej w połowie odległości między a i d)
d – maksymalna wartość, jaką można uzyskać (y przy x dążącym do nieskończoności)

Metoda najmniejszych kwadratów

Metoda najmniejszych kwadratów polega na minimalizacji sumy kwadratów reszt punktów z krzywej (SSE – Sum of Squared Error), którą definiujemy jako:

$SSE = \sum_{i=1}^{n}[y_i - \bar{y}_i]^2$

gdzie:

y_i – wartość y w punkcie i

$\bar{y}_i\text{ - wartość przewidywana przez model w punkcie }\textit{i}$

Implementacja dopasowanie krzywej w Pythonie

Zaczniemy od zaimportowania niezbędnych bibliotek.

Python

import numpy as np
from scipy import stats, polyfit
import sympy as sp
from scipy.optimize import curve_fit
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt

Regresja liniowa

W pierwszej kolejności rozważymy regresję liniową przy użyciu linregress z biblioteki scipy. Zdefiniujmy funkcję obliczającą dodatkowe zmienne. Funkcja (linreg) zwracać będzie słownik zawierający współczynnik R², sumę kwadratów błędu, współczynniki linii regresji i tablice, których użyjemy do rysowania wykresu.

Python

def linreg(x,y):
    res = stats.linregress(x,y)
    
    xmin = min(x)
    xmax = max(x)
    
    # Data for plotting fitted line
    xreg = np.linspace(xmin, xmax)
    yreg = res.intercept + res.slope * xreg
    
    y_predicted = res.intercept + res.slope * x
    # Calculate SSE
    sse = calculate_sse(y, y_predicted)
    
    # Calculate r2
    
    r2 = res.rvalue ** 2
    # Calculate adjusted R-squared
    n = len(y)
    p = 2
    adjusted_R_squared = 1 - (1 - r2) * (n - 1) / (n - p - 1)
    
    return {'x': xreg, 'y': yreg, 'r2': r2, 'intercept': res.intercept, 'slope': res.slope, 'sse': sse,
            'adj_r2': adjusted_R_squared}

Poniższy kod jest przykładem użycia powyższej funkcji.

Python

x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])

linreg_data = linreg(x,y)
plt.scatter(x, y)
plt.plot(linreg_data['x'], linreg_data['y'])
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['Data', 'Linear regression'])
plt.show()

print("R squared:", linreg_data['r2'])

Wielomian

Następnie stworzymy kod do dopasowania wielomianu. Podobnie jak w przypadku regresji liniowej, funkcja zwracać będzie dodatkowe przydatne zmienne w postaci słownika. Podstawową metodą użytą poniżej jest polyfit. Oblicza współczynniki wielomianu. Są one następnie używane do tworzenia funkcji wielomianowej przy użyciu poly1d z biblioteki numpy.

Python

def poly(x,y,degree):
   
    # Perform polynomial fit using scipy's polyfit
    coefficients = polyfit(x, y, degree)

    # Create a polynomial function using the coefficients
    polynomial_function = np.poly1d(coefficients)

    # Generate x values for plotting the fitted curve
    x_fit = np.linspace(min(x), max(x), 40)

    # Calculate y values using the fitted curve
    y_fit = polynomial_function(x_fit)

    # Calculate R-squared (coefficient of determination)
    y_predicted = polynomial_function(x)
    r2 = r2_score(y, y_predicted)
    
    # Calculate SSE
    sse = calculate_sse(y, y_predicted)
    
    xmin = min(x)
    xmax = max(x)
    
    # Calculate adjusted R-squared
    n = len(y)
    p = len(coefficients)
    adjusted_R_squared = 1 - (1 - r2) * (n - 1) / (n - p - 1)
    
    return {'x': x_fit, 'y': y_fit, 'r2': r2, 'coefficients': coefficients, 'sse': sse,
            'adj_r2': adjusted_R_squared}

Użyjmy utworzonej funkcji, aby dopasować ją do wcześniej zdefiniowanych tablic x i y.

Python

poly_data = poly(x,y, 2)
plt.scatter(x, y)
plt.plot(poly_data['x'], poly_data['y'])
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['Data', 'Polynomial regression'])
plt.show()

Online Curve Fitting Tool

Tego narzędzia online można używać do dopasowywania funkcji liniowej, a także takich funkcji jak: wielomianowa, potęgowa i wykładnicza.

Funkcja wykładnicza

Zaprezentowana poniżej funkcja różni się nieco od utworzonych wcześniej. Tutaj używamy metody curve_fit z biblioteki scipy. Możemy jej użyć do dopasowania dowolnej funkcji zdefiniowanej przez programistę. Tutaj używamy funkcji wykładniczej.

Python

def fit_expon(x,y):
    
    # Perform the curve fit

    popt, pcov = curve_fit(exponential_func, x, y, p0=[1.44, 0.35], maxfev=5000)

    # Extract the optimized parameters
    a_opt, b_opt = popt
    
    # Generate fitted values for plotting
    x_fit = np.linspace(min(x), max(x), 40)
    y_fit = exponential_func(x_fit, a_opt, b_opt)
    
    # Calculate the predicted values of y using the fitted parameters
    y_predicted = exponential_func(x, a_opt, b_opt)

    # Calculate R-squared (coefficient of determination)
    r2 = r2_score(y, y_predicted)
    
    # Calculate SSE
    sse = calculate_sse(y, y_predicted)
 
    # Calculate adjusted R-squared
    n = len(y)
    p = len(popt)
    adjusted_R_squared = 1 - (1 - r2) * (n - 1) / (n - p - 1)
    
    return {'x': x_fit, 'y': y_fit, 'r2': r2, 'coefficients': popt, 'sse': sse,
            'adj_r2': adjusted_R_squared}

def exponential_func(x, a, b):
    return a * np.exp(b * x)

Przyjrzyjmy się 5 linii kodu, w której użyto curve_fit:
popt, pcov = curve_fit(exponential_func, x, y, p0=[1,44, 0,35], maxfev=5000)
Widzimy, że funkcja przyjmuje kilka argumentów: funkcję, którą chcemy dopasować (exponential_func), tablice z danymi (x i y), początkowe wartości szukanych parametrów (p0) i maksymalną liczbę wywołań (maxfev). Początkowe wartości szukanych parametrów reprezentują wartości, od których rozpoczną się obliczenia. Funkcja curve_fit zwraca dwie zmienne: popt i pcov:

popt : szacunkowe wartości współczynników krzywej najlepszego dopasowania,
pcov: macierz kowariancji lub błędy.

Dla powyższego dopasowania otrzymujemy:
popt = [3.5351332 0.47297806, 0.47297806]
oraz
pcov = [[ 9.83726219e-02 -2.83133970e-03] [-2.83133970e-03 8.22300127e-05]]

Poniższy kod pokazuje, jak dopasować funkcję wykładniczą i narysować wykres za pomocą biblioteki Matplotlib.

Python

x = np.array([1, 2, 3, 6, 7, 10])
y = np.array([2, 7, 10, 60, 100, 400])
expon_data = fit_expon(x,y)
plt.scatter(x, y)
plt.plot(expon_data['x'], expon_data['y'])
plt.xlabel('x')
plt.ylabel('y')
plt.legend(['Data', 'Exponential fit'])
plt.show()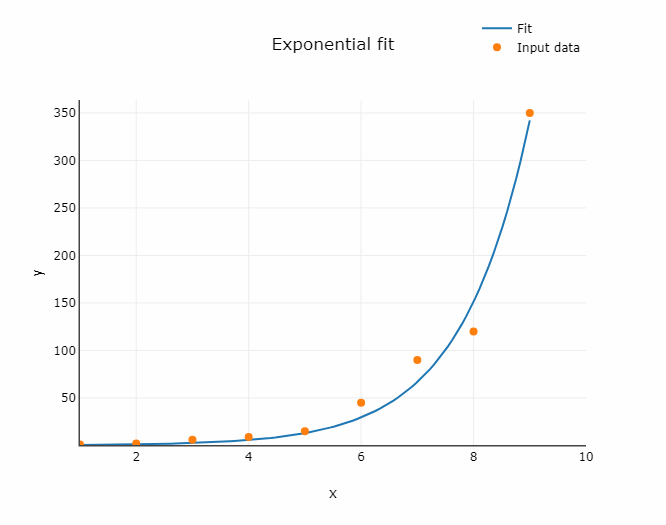

Funkcja potęgowa

Użyjmy utworzonej funkcji, aby dopasować ją do wcześniej zdefiniowanych tablic x i y.

Python

def fit_power(x,y):
        
    # Perform the curve fit
    
    popt, pcov = curve_fit(power_func, x, y, p0=[1.44, 0.35], maxfev=5000)
    # popt, pcov = curve_fit(lambda t, a, b, c: a * np.exp(b * t) + c, x, y)

    # Extract the optimized parameters
    a_opt, b_opt = popt
    
    # Generate fitted values for plotting
    x_fit = np.linspace(min(x), max(x), 40)
    y_fit = power_func(x_fit, a_opt, b_opt)
    
    # Calculate the predicted values of y using the fitted parameters
    y_predicted = power_func(x, a_opt, b_opt)

    # Calculate R-squared (coefficient of determination)
    r2 = r2_score(y, y_predicted)
    
    # Calculate SSE
    sse = calculate_sse(y, y_predicted)
    
    # Calculate adjusted R-squared
    n = len(y)
    p = len(popt)
    adjusted_R_squared = 1 - (1 - r2) * (n - 1) / (n - p - 1)
    
    return {'x': x_fit, 'y': y_fit, 'r2': r2, 'coefficients': popt, 'sse': sse,
            'adj_r2': adjusted_R_squared}


def power_func(x, a, b):
    return a * x ** b

Na koniec przyjrzyjmy się kodowi służącemu do obliczania sumy kwadratów błędów.

Python

def calculate_sse(y_actual, y_predicted):
    # Convert the input lists to NumPy arrays for vectorized operations
    y_actual = np.array(y_actual)
    y_predicted = np.array(y_predicted)
    
    # Calculate squared errors and sum them up
    squared_errors = (y_actual - y_predicted) ** 2
    sse = np.sum(squared_errors)
    
    return sse