Python – regresja liniowa

Wprowadzenie

Regresja liniowa to bardzo prosta i użyteczna metoda matematyczna, stosowana w analizie wszelkich danych. Mówiąc najprościej celem regresji liniowej jest znalezienie równania linii prostej, która najlepiej “pasuje” do zbioru danych x, y. Opis teoretyczny można znaleźć na wielu różnych stronach, między innymi na Wikipedii. Również w tym artykule omówione są teoretyczne aspekty tej metody. Aby się z nimi zapoznać przejdź do sekcji Regresja liniowa: teoria.

Zastosowanie regresji liniowej

Regresja liniowa jest szeroko stosowana w różnych dziedzinach, takich jak ekonomia, nauki społeczne, nauki przyrodnicze, inżynieria itp. O tym jak ważna jest ta metoda świadczy między innymi to, że możemy znaleźć dziesiątki książek poświęconych wyłącznie temu zagadnieniu. Regresja liniowa pojawia się niemal w każdym podręczniku do ekonometrii¹. Również w badaniach naukowych jest ona wykorzystywana bardzo często. Naukowcy starają się znaleźć zależności pomiędzy zmiennymi, dzięki czemu mogą zrozumieć badane zagadnienie. W książce Linear Regression Analysis: Theory and Computing² opisano eksperyment, w którym badano wpływ palenia papierosów na śmiertelność. Możemy również znaleźć inne ciekawe badania naukowe dotyczące zastosowania regresji liniowej. Przykładem może być praca naukowa³, w której wykorzystano tę metodę do określania wieku autora na podstawie pisanych przez niego tekstów.

Biblioteki Pythona do regresji liniowej

W języku Python mamy dwie główne biblioteki, które mogą być wykorzystane do regresji liniowej: scikit-learn oraz statsmodels. Druga z wymienionych jest dużo bardziej rozbudowana i nie będziemy mieli potrzeby korzystać z jej funkcjonalności. Biblioteka scikit-learn zawiera wszystkie kluczowe funkcje na potrzeby większości analiz.
Wykonanie regresji liniowej w Pythonie z użyciem bilbioteki scikitlearn jest bardzo proste. Oprócz tej biblioteki posłużymy się również:

• numpy – biblioteka do obliczeń, w szczególności na macierzach,
• matplotlib – biblioteka do tworzenia wykresów.

Program do regresji liniowej w języku Python

Najpierw zaimportujemy wspomniane biblioteki:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score

Do regresji wykorzystamy dane wygenerowane przy użyciu biblioteki numpy. Wektor X będzie zawierał losowe wartości z przedziału od 0 do 1, natomiast y to wartości obliczone z równania linii prostej, do których dodany będzie losowy “błąd”.

np.random.seed(0)
X = np.random.rand(100, 1)  # Zmienna niezależna
y = 3 * X + 2 + np.random.randn(100, 1)/10  # Zmienna zależna + "błąd"

W następnym kroku utworzymy model regresji liniowej. Metoda LinearRegression() została wcześniej zaimportowana z biblioteki sklearn. Aby dopasować linię prostą do danych X, y, wywołujemy metodę fit().

# Utworzenie modelu regresji liniowej i dopasowanie
model = LinearRegression()
model.fit(X, y)

Do oceny dopasania prostej posłużymy się współczynnikiem R². Z teorii wiemy, że jego wartość powinna być możliwie bliska jedności, co świadczy o dobrym dopasowaniu prostej do danych. Jeżeli wartość jest znacznie mniejsza od jedności (“znacznie” zależy od konkretnego problemu), to pomiędzy danymi X i y nie zachodzi zależność liniowa. Aby wyznaczyć R² najpierw obliczamy wartości y przewidywane przez stworzony model regresji liniowej (metoda predict) dla istniejących wartości X. Następnie otrzymane wartości wykorzystujemy do wywołania metody r2score.

# Wartości przewidywane przez model regresji liniowej
y_pred = model.predict(X)

# Obliczenie R-kwadrat.
r2 = r2_score(y, y_pred)

print("R kwadrat:", r2)

Parametry prostej a*x + b otrzymujemy z atrybutów obiektu model. coef_ to parametr a (nachylenie), a intercept_ to b (przecięcie z osią OY).

# Współczynnik a w równaniu y = a*x + b
a = model.coef_
print("Współczynnik a:", a)

# Współczynnik b w równaniu y = a*x + b
b = model.intercept_
print("Współczynnik b:", b)

W ostatnim kroku zwizualizujemy dane i wyniki. Do tego celu posłuży nam biblioteka Matplotlib. Utworzymy wykres punktowy przy użyciu metody scatter. Metody xlabel i ylabel służą do opisania osi, legend() do utworzenia legendy, na której wyświetlone zostaną wcześniej nadane etykiety (label). Wykres wyświetlamy przy użyciu funkcji show().

plt.scatter(X, y, color='blue', label='Dane')
plt.plot(X, y_pred, color='red', linewidth=2, label='Regresja liniowa')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()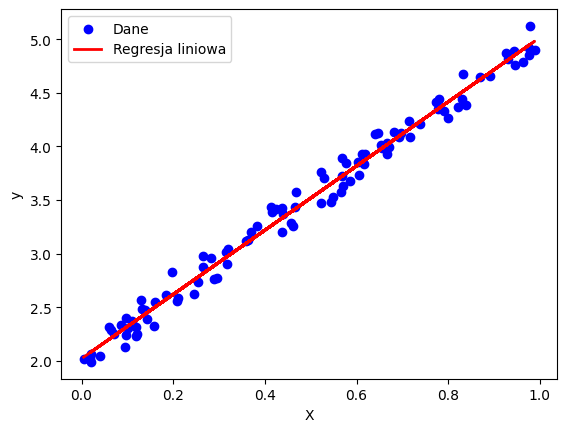

#data science #machine learning #statystyka #analiza danych #python regresja liniowa

Regresję możesz wykonać przy użyciu naszego narzędzia online

Online Curve Fitting Tool

Więcej na temat obliczeń z użyciem Pythona dowiesz się z naszych kursów programowania.

Regresja liniowa: teoria

Regresja liniowa jest metodą statystyczną służącą do określenia zależności między jedną zmienną a drugą (regresja liniowa prosta) lub kilkoma zmiennymi niezależnymi a zmienną zależną (regresja liniowa wielokrotna). Metoda ta znajduje szerokie zastosowanie w różnych dziedzinach, np. w naukach przyrodniczych, ekonomii, medycynie czy naukach technicznych. Obecnie regresję liniową uważa się za jeden z algorytmów nadzorowanych uczenia maszynowego.

Regresja liniowa prosta

Regresja liniowa prosta jest najprostszym przypadkiem regresji liniowej, gdzie analizowany jest związek między jedną zmienną niezależną (X) a jedną zmienną zależną (Y).

Model regresji prostej

Y = β₀ + β₁X

gdzie:

Y – zmienna zależna,

X – zmienna niezależna,

β_0​ – wyraz wolny

β_1​ – współczynnik regresji, określający nachylenie linii regresji,

Interpretacja współczynników

β_0​ to wartość Y, gdy X=0, czyli punkt przecięcia linii regresji z osią Y.

β_1​ to współczynnik nachylenia, mówiący o zmianie Y w odpowiedzi na jednostkową zmianę X.

Przykłady praktycznego zastosowania

O tym jak ważnym zagadnieniem jest regresja liniowa (w tym prosta) świadczyć może fakt powstawania na ten temat podręczników – np. “Applied linear regression”. Do dziedzin, w których wykorzystywana jest regresja liniowa prosta zaliczamy:

• Chemia – analiza wielu zjawisk chemicznych wykorzystuje regresję liniową. Przykładem może być określanie szybkości reakcji chemicznych.
• Ekonomia – przykładem zastosowania regresji liniowej prostej jest badanie wpływu Covid-19 na PKB.

Regresja liniowa wielokrotna

Regresja liniowa wielokrotna służy do określenia zależności między jedną zmienną zależną (Y) a dwiema lub więcej zmiennymi niezależnymi X₁, X₂, …, Xn.

Model regresji wielokrotnej

Y = β₀ + β₁X₁ + β₁X₂ + … + β_nX_n

gdzie:

Y – zmienna zależna,

X₁, X₂, …, Xn – zmienne niezależne,

β_0​ – wyraz wolny

β₁, β₂, …, βn – współczynniki regresji, określające wpływ poszczególnych zmiennych na Y,

Interpretacja współczynników

β_0​ to wartość Y, gdy wszystkie zmienne niezależne X_i​ są równe zero.

β₁, β₂, …, β_n określają jak zmienia się Y w odpowiedzi na jednostkową zmianę poszczególnych X_i, rzy założeniu, że pozostałe zmienne niezależne pozostają stałe.

przy założeniu, że pozostałe zmienne niezależne pozostają stałe

Przykłady praktycznego zastosowania

Możemy znaleźć wiele przykładów zastosowania regresji liniowej wielokrotnej. Poniżej przedstawiamy wybrane:

• Biologia – prognozowanie plonu jęczmienia.
• Sport – identyfikacja czynników wpływających na wyniki drużyny piłkarskiej.

Dopasowanie współczynników w regresji liniowej

Dopasowanie współczynników jest kluczowym procesem w regresji liniowej, który polega na znalezieniu takich wartości, które najlepiej odwzorowują związek między zmiennymi niezależnymi a zmienną zależną. Jedną z metod służących do dopasowania współczynników jest metoda najmniejszych kwadratów.

Metoda najmniejszych kwadratów

Metoda najmniejszych kwadratów polega na minimalizacji sumy kwadratów różnic między rzeczywistymi wartościami zmiennej zależnej a wartościami przewidywanymi przez model, czyli sumę błędu kwadratowego. W przypadku regresji liniowej prostej, minimalizujemy wyrażenie:

Dla regresji liniowej wielokrotnej minimalizujemy analogiczne wyrażenie:

gdzie m to liczba obserwacji.

Ocena dopasowania w regresji liniowej

Zależność wyznaczona poprzez zastosowanie regresji liniowej powinna zostać poddana ocenie, dzięki której będziemy wiedzieć, jak dobrze model regresji liniowej pasuje do danych. Istnieje kilka popularnych miar służących do tego celu. Jedną z nich jest współczynnik determinacji R².

Współczynnik determinacji R²

Współczynnik determinacji R² jest definiowany jako stosunek wyjaśnianej zmienności do całkowitej zmienności zmiennej zależnej:

gdzie:

to obserwowane wartości zmiennej zależnej,
to przewidywane wartości zmiennej zależnej na podstawie modelu regresji,
to średnia wartość zmiennej zależnej,
– to liczba obserwacji.

Wartość R² mieści się w przedziale od 0 do 1, gdzie wartość bliżej 1 oznacza lepsze dopasowanie modelu do danych.

Średni błąd kwadratowy

Średni błąd kwadratowy (MSE – mean square error) to średnia kwadratów różnic między wartością zaobserwowaną w badaniu statystycznym a wartościami przewidywanymi na podstawie modelu. Porównując obserwacje z wartościami przewidywanymi, konieczne jest podniesienie różnic do kwadratu, ponieważ niektóre wartości danych będą większe od przewidywań (a więc ich różnice będą dodatnie), a inne będą mniejsze (a więc ich różnice będą ujemne). Średni błąd kwadratowy obliczamy z zależności:

Podsumowanie

Z tego artykułu dowiedziałeś się czym jest regresja liniowa i jak napisać program, który tworzy model regresji liniowej w Pythonie. W szczególności nauczyłeś się jak:

• wykorzystać bibliotekę scikit-learn do stworzenia modelu prostej regresji liniowej,
• wyznaczyć współczynniki linii prostej oraz współczynnik dopasowania R²,
• narysować wykres z danymi oraz dopasowaną prostą.

Omówione zostały teoretyczne podstawy regresji liniowej wielokrotnej i prostej.

Odnośniki

1. On Using Linear Regressions in Welfare Economics: Journal of Business & Economic Statistics: Vol 14, No 4 (tandfonline.com)
2. Linear Regression Analysis: Theory and Computing | Guide books | ACM Digital Library
3. Nguyen, Dong, Noah A. Smith, and Carolyn Rose. “Author age prediction from text using linear regression.” Proceedings of the 5th ACL-HLT workshop on language technology for cultural heritage, social sciences, and humanities. 2011.