Implementacja regulatora PID w języku Python -

Czym jest regulacja PID?

Regulatory proporcjonalno-całkująco-różniczkujące (PID) są stosowane w przemyśle wytwórczym od lat czterdziestych XX wieku. Regulacja PID jest podobna do regulacji proporcjonalnej, ale z dodatkiem elementów całkujących i różniczkujących. Człon całkujący eliminuje uchyb, podczas gdy człon różniczkujący zapewnia szybką odpowiedź.

Zacznijmy od odrobiny teorii. Poniższe równanie definiuje regulator PID:

$u={{K}_{p}}e(t)+{{K}_{i}}\int\limits_{0}^{t}{e(\tau )d\tau }+{{K}_{d}}\frac{de(t)}{dt}$

$K_{\text{p}}$ , $K_{\text{i}}$ , i $K_{\text{d}}$ oznaczają odpowiednio współczynniki dla członów proporcjonalnego, całkującgo i różniczkującego; e oznacza błąd, a t – czas.

W tym poradniku dowiesz się jak zaimplementować regulator PID w języku Python.

Regulator PID – Przykład zastosowania i implementacji

Układ

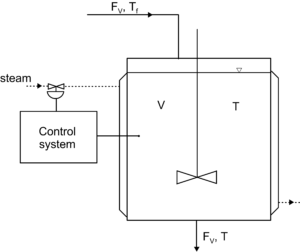
Rozważmy zbiornik służący do ciągłego podgrzewania strumienia cieczy przepływającej przez ten zbiornik z płaszczem grzewczym pokazanym na rysunku. Możemy użyć regulatora PID do uzyskania zadanej temperatury. Posłużymy się prostym modelem matematycznym tego układu (sprawdź dokładniejszy opis tutaj).

$\frac{dT}{dt}=\frac{1}{1+\varepsilon }\left[ \frac{1}{\tau }({{T}_{f}}-T)+Q({{T}_{q}}-T) \right]$

$\varepsilon =\frac{{{m}_{s}}{{c}_{s}}}{V\rho {{c}_{p}}},\ Q=\frac{{{A}_{q}}{{k}_{q}}}{V\rho {{c}_{p}}},\ \tau =\frac{V}{{{F}_{V}}}$

Implementacja kontrolera PID w języku Python

Zacznijmy program od zaimportowania potrzebnych bibliotek.

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt

Będziemy potrzebować kilku zmiennych globalnych, ponieważ obliczenia wymagają historii obiektu.

time = 0
integral = 0
time_prev = -1e-6
e_prev = 0

Poniższa funkcja oblicza wartość zmiennej manipulowanej (MV) na podstawie wartości mierzonej (przykładowo jest to temperatura cieczy) oraz wartości zadanej (temperatury, którą chcemy uzyskać). Funkcja przyjmuje również parametry regulatora.

def PID(Kp, Ki, Kd, setpoint, measurement):
    global time, integral, time_prev, e_prev

    # Value of offset - when the error is equal zero
    offset = 320
    
    # PID calculations
    e = setpoint - measurement
        
    P = Kp*e
    integral = integral + Ki*e*(time - time_prev)
    D = Kd*(e - e_prev)/(time - time_prev)

    # calculate manipulated variable - MV 
    MV = offset + P + integral + D
    
    # update stored data for next iteration
    e_prev = e
    time_prev = time
    return MV

Następnie tworzymy funkcję definiującą układ.

def system(t, temp, Tq):
    epsilon = 1
    tau = 4
    Tf = 300
    Q = 2
    dTdt = 1/(tau*(1+epsilon)) * (Tf-temp) + Q/(1+epsilon)*(Tq-temp)
    return dTdt

Zobaczmy wyniki dla układu bez automatycznego sterowania. Otrzymujemy je rozwiązując przedstawione wcześniej równania różniczkowe.

tspan = np.linspace(0,10,50)
Tq = 320,
sol = odeint(system,300, tspan, args=Tq, tfirst=True)
plt.xlabel('Time')
plt.ylabel('Temperature')
plt.plot(tspan,sol)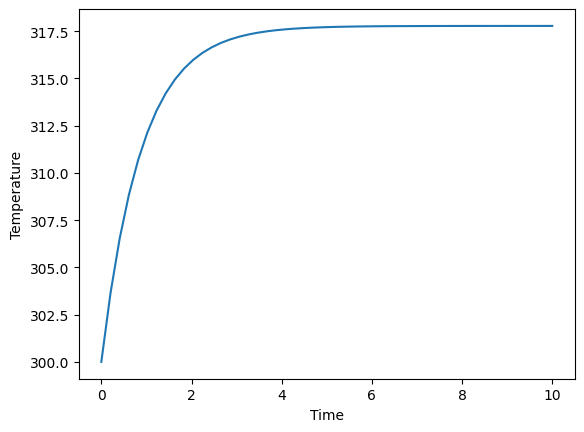

Zmiana temperatury w systemie bez automatycznego sterowania

Widzimy, że temperatura w zbiorniku wynosi początkowo 300 K i stale rośnie do około 317,5. Teraz wykonamy symulację zbiornika ze sterowaniem automatycznym. Powiedzmy, że chcemy osiągnąć temperaturę 310 K. To jest nasza wartość zadana. Parametry regulatora ustalane są dowolnie – można je zmieniać, aby uzyskać wyższą jakość regulacji. Jest to jednak poza zakresem tego przewodnika. Temperaturę czynnika grzewczego wybrano jako zmienną manipulowaną (Tq). Widać, że wartość ta jest obliczana w każdym kroku symulacji z wykorzystaniem wcześniej napisanej funkcji PID.

# number of steps
n = 250
time_prev = 0
y0 = 300
deltat = 0.1
y_sol = [y0]
t_sol = [time_prev]
# Tq is chosen as a manipulated variable

Tq = 320,
q_sol = [Tq[0]]
setpoint = 310
integral = 0
for i in range(1, n):
    time = i * deltat
    tspan = np.linspace(time_prev, time, 10)
    Tq = PID(0.6, 0.2, 0.1, setpoint, y_sol[-1]),
    yi = odeint(system,y_sol[-1], tspan, args = Tq, tfirst=True)
    t_sol.append(time)
    y_sol.append(yi[-1][0])
    q_sol.append(Tq[0])
    time_prev = time

plt.plot(t_sol, y_sol)
plt.xlabel('Time')
plt.ylabel('Temperature')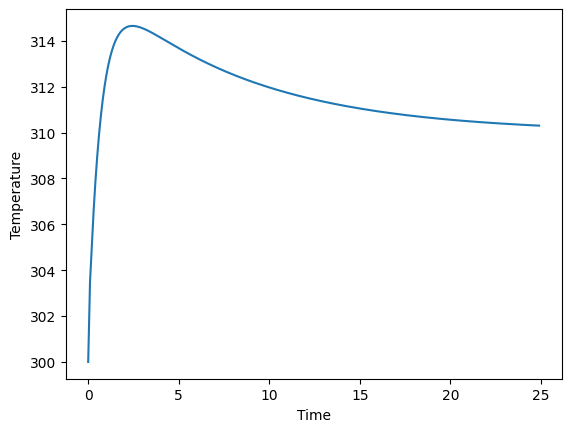

Zmiana temperatury w układzie ze sterowaniem automatycznym

Widać, że regulator sprawia, że temperatura dąży do pożądanej wartości.

Implementacja regulatora PID w języku Python

Czym jest regulacja PID?

Regulator PID – Przykład zastosowania i implementacji

Układ

Implementacja kontrolera PID w języku Python

Plik jupyter notebook znajdziesz na Github.