Definition of Lotka–Volterra model

The Lotka–Volterra (or predator-prey) model is used to describe the dynamics of biological systems in which two species interact (predator and prey). It was formulated in 1926 by famous Italian mathematician Vito Volterra to describe changes in the population of fish in the Adriatic Sea. Independent of Volterra, Alfred Lotka in 1925 derived equivalent equations to describe the oscillations of compound concentrations in a hypothetical chemical reaction. The Lotka-Volterra model is the simplest one of predator-prey interaction.

Lotka-Volterra equations

The model is based on the following assumptions:

only two species exist: predator and prey (for example fox and rabbit),
the rate of change of population is directly proportional to its size,
the predator species is totally dependent on the prey species as its only food supply,
there is no depletion of food for the prey.

The predator-prey model is a system of two ordinary differential equations (Takeuchi, 1996):

$\frac{dx}{dt}=\alpha x-\beta xy$

$\frac{dy}{dt}=\delta xy-\gamma y$

where:

x is the number or population density of prey

y is the number or population density of the predator,
t is time,
α describes the maximum prey’s growth rate,
β describes the effect of predator on the prey’s growth rate,
δ describe the effect of the presence of prey on the predator’s growth rate,
γ describe the predator’s death rate.

Looking at the equations we can see that:

The term αx in the first equation indicates that the prey reproduces exponentially, as it is assumed that the food amount for the prey is always sufficient.
The rate of decreasing the prey’s population (predation) is proportional to the product of the number of preys and the number of predators. It is represented in the first equation as the term βxy. If there is no population of predators, no decrease in the population of prey will can occur.
The predator equation indicates that its growth rate is proportional to product of the number of preys and the number of predators (the term δxy). If there is no predator, no reproduction of predator will occur.
The decrease in predator population is due to natural death (γy).

Simulation of the predator-prey system

Python implementation of the predator-prey model

In order to simulate the system we need to solve a system of nonlinear differential equations. Because of this nonlinearity there is no analytical solution, and we need to find numerical solution. We will use Python programming language to do this.
First we will import necessary libraries.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

Afterwards, we can define the system of differential equations. The function eqs has two arguments: x and t. The argument x consists of the variables, that is the number of predators and preys. Here we will use notation x₁ and x₂ instead of x and y. The function below returns a list dxdt which consists of right-hand-side of the system. The parameters α, β, δ and γ are also defined inside the function. Their values are chosen arbitrarily, but in modelling of real systems they should be chosen based on experiments.

def eqs(x,t):
    # Extract variables
    x1 = x[0]
    x2 = x[1]
    # Define parameters
    alfa = 0.15
    beta = 0.03
    gamma = 0.1
    delta = 0.01

    # Define equations of Lotka-Volterra model
    dxdt = [alfa * x1 - beta * x1 * x2,
            delta * x1 * x2 - gamma * x2]
    return dxdt

Now we can obtain the solution. We will use odeint function from scipy library, which is used to solve a system of ordinary differential equations. First, we set the initial conditions. It is a list of number of preys and number of predators, respectively. The function odeint accepts three arguments: function defining the equations, the list defining the initial conditions and the list of time values. The solution consists of two functions: x(t) and y(t), or in other words dependencies of predator and prey populations on time.

# Set initial conditions
y0 = [50, 10]

# Set the time grid
t = np.linspace(0, 360, 500)

# Solve the ODE system
sol = odeint(eqs, y0, t)

Finally, we can plot the results using matplotlib library.

# Extract the solution variables for plotting
x1 = sol[:, 0]  # extract the first variable
x2 = sol[:, 1]  # extract the second variable

# Plot the solution
plt.plot(t, x1, label='Prey')
plt.plot(t, x2, label='Predator')
plt.xlabel('Time')
plt.ylabel('Number')
plt.legend(loc='upper right')
# Set the maximum y-value on the plot
plt.ylim(0, np.max(x1) + 10)
plt.grid(True)
plt.show()

Simulation of Predator-Prey system (Volterra-Lotka model) — Fig. 1. Simulation results of predator-prey system (Lotka-Volterra model)

Predator-prey population dynamics

From the Fig. 1 we can clearly see that the prey and predator populations oscillate. The predator population increases when food (prey) is available. However, it causes the drop of prey population and as a result the predator number also decreases. Such conditions are favorable for the reproduction of the prey. And the situation repeats over and over. Real biological systems with species interacting in a predator-prey way also exhibit oscillations, but the interaction is much more complex (Yoshida et al., 2003). Lotka-Volterra predator-prey model is still valuable for understanding how biological systems work and it is used for developing more advanced mathematical models (Tabiś and Skoneczny, 2013).

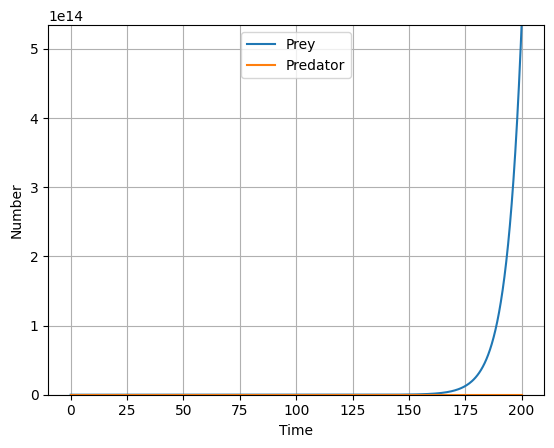
Prey population dynamics in the absence of predator

We can use the model to analyze a hypothetical case with the predator dynamics equal zero. To do this, we only need to set its initial population to zero, as in the code below.

# Set initial conditions
y0 = [50, 0]

The rest of the code is the same as previously. Let’s analyze the results shown in Fig. 2. We can see that the predator number is always zero what arises from its initial value. Despite that there is food (prey) available, the reproduction of predator cannot occur. Clearly, the prey population growth is exponential. As the model assumes limitless food for the prey there is no factor limiting its population (no predation and prey death is neglected in the model). It is also reflected in the differential equation for y = 0: x‘ =α x.

Fig. 2. Prey population dynamics with the absence of predator

Download Jupyter notebook

References

Takeuchi, Y. (1996). Global Dynamical Properties of Lotka-Volterra Systems. World Scientific. Google books link

Yoshida, T., Jones, L. E., Ellner, S. P., Fussmann, G. F., & Hairston Jr, N. G. (2003). Rapid evolution drives ecological dynamics in a predator–prey system. Nature, 424(6946), 303–306. Link

Tabiś, B., & Skoneczny, S. (2013). Stabilization of unstable steady states of a continuous stirred tank bioreactor with predator–prey kinetics. Journal of Biotechnology, 166(4), 145–151. Link

Lotka-Volterra model and simulation